Amit a hang(kártyák)ról tudni érdemes

Mostanában a videokártyák, alaplapok és RAM-ok mellett igen elhanyagolt téma a hangkártyák világa (régebben viszont igen népszerű "csatatér" volt ez, gondoljunk csak vissza a SB-, illetve GUS-hívők viaskodásaira), bár az is igaz, hogy túl sok, az átlagos felhasználót érintő változás nem történt. Egy összefoglaló viszont -- én legalábbis így gondolom -- nem árthat, annál is inkább, mert ilyesmi nemigen található a neten, és talán sokakat segít eligazodni a jövőben.

Természetesen nem törekszem teljességre (ezt nem is nagyon lehetne), és a hozzáértőktől előre is elnézést kérek a néha pongyola fogalmazásért (bár próbálom kerülni): elsősorban azt szeretném, hogy az itt leírtak közérthetőek legyenek, már amennyire ez lehetséges.

Hang - idő és frekvencia

Mint valószínűleg mindenki tudja a hang valamilyen rugalmas közeg mechanikai rezgése. A levegőben terjedő hang nyomásingadozás formájában jelentkezik, a (nagyjából) állandó légköri nyomáshoz adódik hozzá egy időben változó nyomás, ezt nevezzük hangnyomásnak, a továbbiakban csak a ezzel foglalkozom.

Az időben változó nyomás leírható az amplitúdó időbeli változásával -- azaz egy olyan függvénnyel, amely megmondja, hogy az egyes időpillanatokban mekkora a nyomás. Nézzünk például egy szinuszhangot (azzal úgyis sokat fogunk foglalkozni, a szinuszfüggvényről meg remélhetőleg már mindenki hallott):

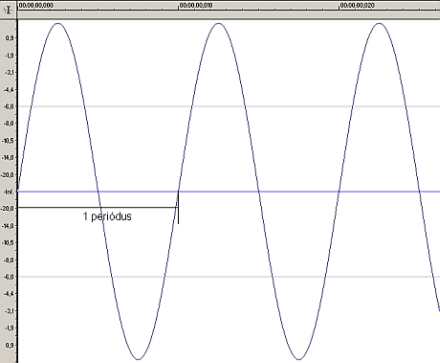
A hang egy mind időben, mind amplitúdóban folytonos folyamat,azaz az összes időpontban van amplitúdóértéke, ami tetszőleges lehet. Fontos itt megismerni egy másik leírást: a frekvenciatartománybelit. Induljunk az elejéről! A frekvencia definíció szerint (periodikus, azaz ismétlődő függvényekre/jelekre) az időegység alatti periódusok (ismétlődések) száma: tehát egy 500 Hz-es szinuszjelnek 500 periódusa esik az egy másodperces időintervallumba. Általában kevésbé ismert, de tény, hogy minden periodikus jel felbontható (megfelelően eltolt) szinuszok összegére: tehát például egy háromszögjel felírható akárhány szinusz összegeként (minél több komponenssel írjuk le, annál pontosabban kapjuk vissza az eredeti háromszögjelet). Az erre szolgáló matematikai formula a Fourier sorfejtés.

A Fourier sorfejtés kiterjesztése végtelen hosszú periódusidejű jelekre (azaz nem periodikus jelekre) a Fourier integrál. Az időtartománybeli függvény Fourier integrálásával kapott függvényt nevezzük a jel spektrumának, ami egy komplex függvény. Ennek abszolútértéke az amplitúdóspektrum, míg arcusza a fázisspektrum. Előbbi felfogható úgy, mint azt az előbb tettük, tehát megmondja, hogy az egyes frekvenciájú szinuszkomponenseket milyen amplitúdóval kell összegezni ahhoz, hogy visszakapjuk az eredeti jelet, utóbbi pedig meghatározza, hogy az egyes szinuszkomponenseket mennyivel kell késleltetni. Szinuszjel esetében a spektrum (értelemszerűen) egyetlen vonalból áll, a szinusz frekvenciájának megfelelő helyen, hiszen ezt az egy komponenst véve megkapjuk a jelünket.

[oldal:Spektrum, decibel]

Nézzünk egy példát egy picit bonyolultabb jel spektrumára: legyen a jelünk egy háromszögjel (a vízszintes tengely az idő, a függőleges az amplitúdó):

Ennek amplitúdó-spektruma pedig:

Nem látszik túl jól, ezért inkább elmondom. Az eredeti jel 500Hz-es háromszögjel volt (tehát periodikus). A spektrumában szerepel egy, az eredeti jellel azonos frekvenciájú összetevő (500 Hz, ez az alapharmonikus), ezen kívül pedig minden olyan frekvencián megjelenik komponens, amely az alapharmonikus páratlan számú többszöröse (1500, 2500, 3500... Hz, ezek a páratlan felharmónikusok, háromszögjel esetén nincsenek páros felharmonikusok).

A zajtól eltekintve jól látszik, amit az előbb említettem: periodikus jelek előállíthatók szinuszjelek összegeként, ami azt jelenti, hogy a spektrumukban csak az alapharmónikus többszöröseinél lehet komponens, a spektrum vonalas, diszkrét (azaz csak meghatározott helyeken vehet fel értéket). Nem periodikus jelek esetén a spektrum nem vonalas, hanem folytonos, minden frekvencián találhatunk komponenst. A mély hangok az alacsony frekvenciásak, a magasak pedig a (meglepetés!) magas frekvenciásak.

Rögtön még itt az elején meg kell említeni a deciBel (dB) fogalmát (majd a jel/zaj viszony mérésénél lesz fontos). A Bel teljesítmény jellegű mennyiségek arányának tízes alapú logaritmusa, a decibel ennek tizede (képlettel: dB=10*lg (P/Palap)). Semmi ördöngösségre sem kell gondolni, egyszerűen van egy viszonyítási alap, amellyel az adott (mondjuk mért) teljesítményt elosztva, majd tízes alapú logaritmusát képezve és ezt tízzel megszorozva megkapjuk a teljesítménynek megfelelő decibelértéket. Tehát például ha a viszonyítási alap 1 W (watt), én pedig valahol mértem 1000 W-ot, akkor ez deciBelben kifejezve 30. Ha ugyanezt nem teljesítménnyel, hanem mondjuk feszültséggel tenném, akkor a helyzet a következő:

Mivel a deciBel teljesítmény jellegű mennyiségekre lett definiálva, használjuk fel, hogy a teljesítmény a feszültség négyzetével (a feszültség amplitúdó jellegű mennyiség, csakúgy mint a nyomás) arányos. Így a logaritmuson belül nem két teljesítmény aránya, hanem két feszültség négyzetének aránya áll, egyébként a képlet ugyanaz. A négyzetre emelés viszont kihozható a logaritmus-képzés elé, egy kettes szorzóként, tehát amplitúdó jellegű mennyiségekre a képlet: dB=20*lg (U/Ualap).

Ebből rögtön látható, a dB legfontosabb előnye: mindegy hogy teljesítményt vagy amplitúdót helyettesítek (a megfelelő képletbe), az eredmény nem változik. Az például, hogy egy hangkártya jel/zaj viszonya (SNR) 80 dB azt jelenti, hogy a jel teljesítménye százmilliószor akkora, mint a zajé (ha jól számoltam).

Most remélhetőleg már mindenkinek van némi elképzelése a spektrumról, meg a dB-ről is, ugorjunk egyet. Mint azt említettem, a hang egy időben és amplitúdóban folytonos jel, a számítógépen viszont csak diszkrét jeleket tudunk tárolni (ezt azt hiszem nem kell magyarázni). Az időbeli diszkretizálást mintavételezésnek, az amplitúdóbelit pedig kvantálásnak nevezzük.

[oldal:Mintavételezés, kvantálás, átvitel]

A mintavételezés jelentése a következő: az adott időfüggvényből valamilyen időközönként (mintavételezési idő) mintákat veszünk, és ezeket tároljuk (az amplitúdó itt még folytonos!). Felmerül a kérdés, hogy milyen hatással lesz ez a jelünkre. Hosszasabb bizonyítás nélkül a Shannon tétel: ha egy jel sávkorlátozott, akkor a sávkorlát kétszeresénél nagyobb frekvenciával mintavételezve nem veszítünk információt (a mintavételezési frekvencia a mintavételezési idő reciproka). Nézzük szép sorjában! A sávkorlátozott jel azt jelenti, hogy egy B (ez a sávkorlát) frekvenciánál nagyobb frekvenciákon a spektrum nulla (tehát ott nincs spektrális komponens). A szomorú az, hogy amelyik jel időben véges (márpedig az ember ritkábban foglalkozik végtelen hosszú jelekkel), az spektrálisan végtelen (és fordítva: spektrálisan véges -- azaz sávkorlátozott -- jel időben végtelen). Egy picit azonban mázlink van, mert az emberi fül hallástartománya véges, tipikusan azt szokták mondani, hogy 20 Hz-től 20 kHz-ig hallunk (már aki), így a 20 kHz-nél magasabb frekvenciákat nincs értelme tárolni, hiszen azt úgysem halljuk (egyesek szerint viszont érezzük, de ebbe itt most nem megyünk bele). Tehát a hangokat tekinthetjük olyan jeleknek, melyek sávkorlátja 20kHz, így a Shannon tétel értelmében minimum 40 kHz-el kell mintavételezni. De...

Megint csak bizonyítás nélkül (mint minden): a mintavételezett jel spektruma megegyezik az eredeti (folytonos jel) spektrumával, annyi különbséggel, hogy a mintavételi frekvenciára periódikusan ismétlődik az eredeti spektrum (tehát egy, a frekvenciában periodikus jelünk van). Ha ehhez még azt is hozzáteszem, hogy valós jelekre a spektrum a nulla frekvenciatenglyre szimmetrikus, akkor a Shannon tétel már szemléletesen is látható:

A vízszintes tengely a frekvencia, a függőleges az amplitúdó. Aki még nem látott ilyen ábrát az nézegesse egy picit, jól látszik, hogy az eredeti analóg jel spektruma a mintavételi frekvenciával (fs) periodikus (B a sávkorlát). Képzeljük el azt az esetet, amikor az analóg jel nem sávkorlátozott (vagy a mintavételi frekvencia kisebb, mint a sávkorlát kétszerese). Ekkor az analóg spektrum megintcsak ismétlődik a mintavételi frekvenciával, a különbség annyi, hogy az eredeti spektrum és az ismétlődések nem különülnek el ilyen szépen, hanem egymásba lapolódnak: ezt a jelenséget nevezik aliasingnak, ekkor nem megállapítható, hogy egy adott komponens az eredeti spektrumból származik-e vagy átlapolódás során jött létre. Tehát a Shannon tételt be kell tartani, különben torzul a spektrum.

Abban viszont nem lehetünk biztosak, hogy azért mert nem halljuk, nincs is magasabb frekvenciás komponens, ezek kiszűréséről gondoskodni kell, erre szolgál az analóg-digitális átalakító bemenetén egy aluláteresztő szűrő (az aluláteresztő szűrő annyit tesz, hogy egy bizonyos frekvenciáig átengedi magán a jelet, e felett pedig nem), az ún. anti-aliasing filter. Ez a szűrő az oka, hogy a tipikus mintavételi frekvencia nem 40, hanem mondjuk 48 kHz, ugyanis olyan szűrőt nem lehet csinálni, ami 20 kHz-ig átenged, e felett viszont nem, csak olyat, ami 20 kHz-ig átenged, ott elkezd csillapítani, és 24-28 kHz környékén a csillapítása már elég nagy ahhoz, hogy úgy tekintsük, mintha nem engedne át (na jó, igazság szerint erről hosszabban is el lehetne elmélkedni, inkább maradjunk annyiban, hogy ténylegesen megvalósított átalakítókban a mintavételi frekvencia akár négyszer akkora is lehet, mint a sávkorlát -- és akkor még nem beszéltünk a szigma-delta átalakítókról --, mert így az anti-aliasing szűrő, ami analóg, specifikációi kicsit enyhébbek, ezt pedig könnyebb megvalósítani). Ennyit a mintavételről, nézzük a kvantálást!

A kvantálás a folytonos amplitúdó értékek diszkrétté alakítása (hiszen például ha 16 biten szeretnénk tárolni a hang amplitúdót, ez azt jelenti, hogy 65536 különböző értéket tudunk megkülönböztetni, nem pedig végtelen sokat). A kvantálás legnagyobb baja, hogy még elvben sem képzelhető el olyan eset, amikor kvantálással nem veszítünk információt, tehát mindig információvesztéssel jár. A kérdés: mégis hány biten ábrázoljuk az adatainkat? A kvantálás okozta zavaró hatás jól leírható a jel/zaj viszonnyal (ami jel és a zaj teljesítményének viszonya dB-ben). Hosszasabb magyarázat nélkül egy n bites átalakító (elvi) jel/zaj viszonya: SNR=6,02n+1,74 dB. Adott átalakítót vizsgálva a mért jel/zaj viszonyból ezzel a képlettel visszaszámolt bitszámot effektív bitszámnak nevezzük. Mivel 140 dB-nél nagyobb dinamikára nincs szükség (ez az emberi fájdalomküszöb), így visszaszámolható, hogy 24 bites átalakítókat használva a végeredmény teljesen megfelelő lesz.

Az átvitel

A hangkártyát tekinthetjük egy fekete doboznak: nem tudjuk mi van benne, csak azt, hogy ha valamilyen jelet adunk a bemenetére, arra mi a kimenet. Egy ilyen rendszert jellemezhetünk az átviteli karakterisztikájával (kimenet spektruma=bemenet spektruma*átviteli karakterisztika). Ez is egy komplex függvény, melyet megint csak két részre bonthatunk, az első a frekvencia - amplitúdó (amplitúdókarakterisztika), a második pedig a frekbencia - fázis (fáziskarakterisztika).

Az amplitúdókarakterisztika azt mutatja meg, hogy a rendszer bemenetére érkező bizonyos frekvenciájú jelek mennyit erősödnek, illetve gyengülnek, miközben áthaladnak a rendszeren, míg a fáziskarakterisztika megadja, hogy egy bizonyos frekvenciájú jelet mennyivel késleltet a rendszer. Igazán az lenne az ideális, ha a kimenő jel alakja nem térne el a bemenő jel alakjától, ezt az esetet nevezzük alakhű átvitelnek. Ahhoz hogy egy rendszer alakhű átvitelt valósítson meg, amplitúdókarakterisztikájának egy vízszintes egyenesnek, fáziskarakterisztikájának pedig egy ferde egyenesnek kell lennie (kevésbé pongyolán: az amplitúdókarakterisztika konstans, a fáziskarakterisztika pedig lineáris).

[oldal:3D-s hangzás]

Csak nagyon alapszinten nézzük meg, hogyan is képez a hangkártya 3D-hangot!

Az agy a hangforrás irányát alapvetően abból dekódolja, hogy a két fülbe milyen időkülönbséggel érkezik meg ugyanaz a hang (Inter-Aural Time Delay). A dolgot tovább árnyalja, hogy a hang nem csak közvetlenül jut a hangforrástól a fülbe, hanem (még ha a környezettel most nem is foglalkozunk) az egyéb testrészekről (váll, fej...) visszaverődve, torzulva. Ezeket a hatásokat egy, az emberi fejre/testre jellemző függvénnyel, a HRTF-el (Head Related Transfer Function) írják le. Ez (a változatosság kedvéért) megintcsak egy átviteli karakterisztika, aminek bemenete a gerjesztő jel (tehát a hangforrás jele), kimenete pedig az a jel, amit az emberi fül érzékel (az iránynak, távolságnak megfelelően). Egyszerűbb (kevésbé igényes) esetekben megelégednek a panning alapú irányérzet keltéssel: minél inkább jobbra van a hangforrás, a jobb hangszóró annál hangosabb, a bal pedig egyre halkabb (ez persze kissé igénytelen megoldás, és pocsék a minősége).

A HRTF függvények készítése meglehetősen hosszadalmas. Egy süketszobába (olyan szoba, ahol nincs hangvisszaverődés, sem a falakról, sem a padlóról..., elég nyomasztó hely) helyezzünk el egy műfejet, rajta két műfüllel (ezek az emberi szerveket utánozzák). A két műfülbe helyezzünk egy-egy mikrofont. A műfej körül egy gömbön mozgatva a hangszórót, megmérhetjük, hogy az egyes hangforrás-pozícióktól és a frekvenciától függően mit hall az ember. Innentől kezdve a feladat leírva egyszerű, kivitelezve bonyolult: olyan algoritmust kell találni, ami ugyanezt az érzetet kelti a fülben (HRTF).

Bármilyen meglepő, fülhallgatót feltételezve a legegyszerűbb a dolog, hiszen a feladat csak annyi, hogy a gerjesztő jel (a hangszóró jele) és a fülekben mért jelek között kapcsolatot találjunk: azaz egy olyan átviteli függvényt kell alkotni, ami a gerjesztő jelből a fülben mérhető jelet produkálja, a két fülre külön-külön.

Két és négy hangszóró esetén a helyzet egy kicsit bonyolultabbá válik, hiszen mindkét fülünk hallja az összes hangszóró jelét (persze nem egyformán), így nem lehet ugyanazt megtenni, mint fülhallgató esetén. Ilyenkor szokás Cross-Talk-Cancellationt használni, ami pont ezt a hatást szünteti meg.

Megvan már a hangforrás iránya, de hiányzik még a távolsága. Egyrészről az teljesen igaz, hogy egy adott amplitúdójú ("hangosságú") hangforrástól távolodva a hangosság-érzet egyre csökken, viszont ez egyszerűen beláthatóan nem elég a hangorrás távolságának detektálásához. Képzeljünk el egy hangforrást, ami igen hangos, de messze van tőlünk (az érzékelt "hangosság" legyen mondjuk 42). Most hozzuk közel a forrást, de halkítsuk le (úgy, hogy az érzékelt "hangosság" legyen ugyanakkora, mint az előbb).

A fentiek tükrében azt gondolhatnánk, hogy a fülünk nem tud különbséget tenni a két forrás között. Egyszerű oka van, hogy ez mégsem igaz: a környezet, pontosabban a környezetünkben lévő tárgyakról visszavert hangok. Az agy a visszavert és a közvetlen úton a fülbe jutott hangok arányából képes a távolság pontosabb meghatározására (ezt nevezik DDR-nek, Direct to Reverberant Ratio).

Ebből is látható, hogy az EAX illetve az A3D2 nem csak akkor fontos, amikor mondjuk egy zengő barlangba lépünk: az ideális az lenne, ha minden játék használná.

[oldal:Hangszintézis - FM szintézis]

Bár manapság játékokban nem nagyon találkozhatunk MIDI zenével, a módszert (a játékok szempontjából) mégsem kell elvetni. Pozitív hozzáállásom oka a DirectMusic, ami lehetővé teszi, hogy a cselekmény hatására dinamikusan változzon a zene. A széles körben tapasztalt lekicsinylő hozzáállás oka a MIDI azonosítása a pocsék minőségű szintetizálással. A MIDI pedig nem ez.

Nagyon leegyszerűsítve a MIDI file-ok nem a rögzített hangot, hanem csak üzeneteket tartalmaznak: mikor melyik hangszer milyen hangosan, melyik hangmagasságon, mennyi ideig szólaljon meg (meg még sok egyéb, de a MIDI szabványt nem ismertetném, ha nem baj :)). Az hogy a megszólaló zene milyen minőségű lesz csak és kizárólag a szintetizálást végző hangkártyától (vagy szoftvertől) függ. Tekintsük át röviden milyen módszerek léteznek!

FM szintézis

Az első, széles körben elterjedt módszer, az első AdLib és SoundBlaster kártyáktól kezdve egészen a SoundBlaster AWE32 megjelenéséig ez volt a legtöbb PC-s (játékosoknak szánt) hangkártyán megtalálható szintetizátor, és ebben az időben alakult ki a MIDI zenével kapcsolatos ellenérzés. Mi tagadás, ennek volt is alapja, az FM szintézis ugyanis élethű hangvisszaadásra nem kifejezetten alkalmas. Az FM rövidítés a frekvencia modulációt takarja: egy jelnek a frekvenciát egy másik jellel változtatjuk (moduláljuk).

Az FM szintézis felfedezése a francia IRCAM zenekutató intézet nevéhez fűződik. Itt vették észre először, hogy ha a moduláló forrás frekvenciáját a 100 Hz-es tartományra növelik, akkor eltűnik a vibrato hatás (ld. Wavetable szintézis), és az ember a hang színén érez változást.

Az FM lényege, hogy nem egy felharmonikusokban gazdag jelből indulunk ki, hanem egyszerű hullámformákból, s ezt moduláljuk. A modulálandó, azaz a vivő a carrier, míg a moduláló forrás a modulátor (összefoglaló nevük pedig operátor). A modulátor hatására újabb frekvenciakomponensek (ún. sidebands) keletkeznek az alapfrekvencia (a carrier frekvenciája) alatt és felett.

A sidebandek, a carrier/modulátor frekvenciaaránya és a modulátor amplitúdója (ill. a modulációs index) között precíz kapcsolatot a Bessel-függvények teremtenek, de általában elfogadható közelítés, hogy a carrier frekvenciája alatt és fölött is a modulációs index+2 számú sideband jön létre. A sidebandek frekvenciája pedig f=carrier-frekvencia +/- (modulátor frekvenciája*k), ahol a k a sideband sorszáma, 0 és (modulációs index+2) között minden egész értéket felvesz.

A pontos összefüggést most kihagynám, egyrészt igen macerás lenne begépelni, másrészt teljesen érdektelen (és ronda egy képlet, majd' két sor). FM szintetizátorokban általában a következő egyszerű hullámformák választhatók ki:

• szinusz
• fűrészfog: az alapharmonikus összes felharmonikusát tartalmazza, az n-edik felharmonikus amplitúdója n-ede az alapharmonikus amplitúdójának háromszög: a fűrészfog-jelhez hasonló, de a felharmonikusok amlitúdója exponenciálisan csökken
• négyszögjel: az alapharmonikus páratlan számú többszöröseit tartalmazza, az (2n-1)-edik felharmonikus amplitúdója az alapharmonikus amplitúdójának (2n-1)-ede.

A 8 bites SB-k korában két operátort lehetett egy hangszer szintetizálásához felhasználni, modernebb szintetizátorokban ennek többszöröse is elképzelhető, sőt az operátorok tetszőlegesen őszzekapcsolhatók. A módszer legnagyobb baja, hogy igen nehéz úgy programozni, hogy egy elképzelt hullámforma létrejöjjön, enélkül pedig maximum új, nem létező hangzások készítésére jó (arra viszont nagyon), ezért található meg jópár hangszerkesztő programban szoftveres megvalósítás (az elkészített hangzás pedig wavetable szintetizátorokban használható).

[oldal:Hangszintézis - Wavetable szintézis]

Mivel ma szinte egyeduralkodó módszer a PC-s hangkeltők körében, ezért ezzel bővebben foglalkozom (lehet örülni, esetleg átugrani). Kezdjük egy pár fogalom tisztázásával:

Polifónia: egy szintetizátor polifón, ha képes egyidejűleg több hangot különböző hangmagasságokon megszólaltatni (például az emberi hang nem polifón, hiszen egyszerre csak egy hangmagasságon szól). A polifóniafok jelenti az egyszerre megszólaltatható hangok számát.

A multitimbralitás foka azt adja meg, hogy egy szintetizátor hány különböző hangszer hangját képes egyszerre megszólaltatni.

Sample (minta): a digitalizálásnál kapott egyetlen, a kvantálási szintre kerekített amplitúdóérték

Waveform (hullámforma, hangminta): sample-ök összessége, számuk (a hangminta időtartama)*(a mintavételi frekvencia)

Patch: egy vagy több hullámforma, valamint az ezekhez tartozó vezérlőinformációk összessége (LFO-k, EG-k, szűrők vezérlőinformációi)

Root-key: egy hangmintának a root-key-je az a hangmagasság, ahol a hangmintát digitalizáltuk

MIDI (Musical Instruments Digital Interface): a szabvány meghatároz alapvető követelményeket, amelyeket egy szintetizátornak teljesítenie kell (24-szeres polifónia, 16-szoros multitimbralitás), valamint egy 128 melodikus és 60 dobból álló hangszerkészletet

A wavetable szintetizátorok az egyes hangszerek digitalizált mintáival dolgoznak, melyeket ROM-ban vagy RAM-ban tárolnak A hangszerek hangját tulajdonképpen úgy generálják, hogy a digitalizált hangot lejátszák. Mégsem csak egy egyszerű visszajátszás ez, hiszen lehetőség van a hang paramétereinek változtatására, valamint egy sor probléma is felmerül. De az tény, hogy szintetizálásról -- abban az értelemben, hogy a "semmiből" létrehozunk valamit -- nem beszélhetünk.

Az első probléma az, hogy hogyan képezzük az egyes hangmagasságokat. Nyilván az lenne a legjobb, ha egy hangszerről az összes hangmagasságon mintákat vennénk. Ekkor azonban egy kilenc oktávot átfogó hangszernél 117 hangmintára lenne szükség, ami 44,1 kHz-es mintavételi frekvenciát és 16 bites felbontást feltételezve 10 Mbyte-nyi adatot jelentene, ha minden hangminta csak egy másodperc hosszúságú. Ha mindezt a MIDI szbványban foglalt 128 hangszerre elvégezzük, 1280 Mbyte-nyi ROM-ra illetve RAM-ra lenne szükség, ami kissé megdrágítaná a szintetizátorokat (még a mai memóriaárak mellett is).

Az sem elegendő viszont, ha minden hangszerről csak egy hangmintát tárolunk és ebből állítjuk elő a többi hangmagasságot, hiszen például a zongora hangja teljesen más a mélyebb, mint a magasabb tartományokban (mély hangoknál a húr rezgése, magasabbaknál a kalapács ütődése a domináns). A megoldás az ésszerű multisampling (azaz több mintát tárolunk). Így lehetőség van arra, hogy a magasabb hangokat egy magasabb hangmintával, a mélyebbeket pedig egy mélyebbel szintetizáljuk.

Így egy újabb problémához jutunk. Lesz tehát egy olyan hangmagasság, aminél a mélyebbeket (például E5 és alatta) egy mély (pl. C4) root-key-ű hangmintával, a magasabbakat ( F5 és felette) pedig egy magas root-key-ű (pl. D6) hangmintával generáljuk. Ekkor minden E5-F5 váltásnál úgy fogjuk érezni, hogy másik hangszer szólal meg. Erre jelent megoldást a multilayering egy alkalmazása.

A multilayering lehetőséget ad arra, hogy minden hangmagassághoz több hangmintát rendeljünk. Így például megoldható, hogy az E5 alatti hangmagasságokon is szóljon mind a C4, mind a D6 root-key-ű minta, de az E5-től a mélyebb hangok felé haladva fokozatosan a C4 legyen a dominánsabb (ennek hangereje növekedjen, a másik mintáé csökkenjen). Ehhez a szintetizátor részéről szükséges, hogy az amplitúdó burkolót a hangmagassággal lehessen vezérelni.

Egy adott hangmagasságú hangot a mintavételi frekvencia kétszeresével lejátszva egy oktávval magasabb hangot kapunk, fele akkora frekvenciával lejátszva pedig egy oktávval mélyebbet. A szintetizátorok (legalábbis nagy többségük) mégsem így képezik a más hangmagasságú hangokat, hiszen így például két oktáv emeléséhez 176,4 kHz-es lejátszási frekvenciára lenne szükség.

Ehelyett ha magasabb hangra van szükség (például egy oktávval magasabbra), akkor decimál a szintetizátor (minden második mintát elhagy), és 44,1 kHz-el játszik le, ha mélyebb hangra van szükség, akkor pedig minden minta után interpolál egy újat, a lejátszási frekvencia pedig változatlan marad. A jó algoritmus az, hogy meghatározzuk a transzponált és a transzponálandó hang (azaz a root-key) frekvenciájának hányadosát (ez egy oktáv emelésnél például 2), majd ezt X/Y törtalakra hozzuk (ahol X,Y egész). Ezután minden minta után interpolálunk X számú új mintát, majd minden minta után elhagyunk Y számú mintát.

[oldal:Hangszintézis - Wavetable szintézis - folytatás]

A minőséget nagyban befolyásolja az interpolálás minősége. Régebben a lineáris interpoláció volt meghatározó, ahol az új mintákat úgy számítjuk, hogy két meglevő mintára egy egyenest fektetünk, és ennek a megfelelő időpillanatban vett értékei lesznek az új minták. Picit szemléletesebben egy ábra:

Mai modernebb hangkártyákban ennél magasabb fokú interpolációt alkalmaznak (az SB Live! kártyák EMU10k1 processzora például nyolc pontost), ami azt jelenti hogy az interpolált minták számításához az eredeti mintákból nem kettőt hanem jóval többet használnak fel.

Nyilvánvalóan vetődik fel a következő probléma. A tárolt hangminta hossza véges, amikor viszont a szintetizált hangszert használjuk biztos, hogy nem pont ilyen hosszú ideig kell szólnia. A megoldás a loopolás.

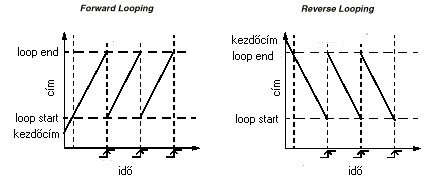
Minden hangszernek van egy kitartási fázisa (a burkológörbe sustain szakasza), amely alatt a hang tulajdonságai elhanyagolható mértékben változnak. Ebből a fázisból egy rövid részt ismételgetve tetszőleges ideig szólhat a hang. Amikor a lejátszás eléri a loop end pontot, visszaugrik a loop start pontig, és így tovább, amíg a hangszert gerjesztik.

A jó loop-pontok megtalálása nagyon nehéz, ha az ismétlődő rész túl rövid, a hang elveszti jellegzetességeit, ha pedig túl hosszú, akkor már nem hanyagolhatók el a szakasz alatt végbemenő változások. Utóbbi problémára jelent megoldást a bidirectional loop. Ennél a típusnál a lejátszás tart a loop endig, itt azonban a lejátszás iránya megfordul, tart a loop startig, ahol ismét megfordul. Ez a loopolási módszer csak palindróm ("szimmetrikus") hullámformák esetén alkalmazható, hiszen visszafelé játszva is ugyanazt a hangot kell kapnunk.

Az alábbi ábra a három loop-típust mutatja.

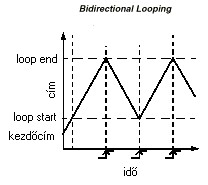
Felmerült már, hogy a hang amplitúdója időben nem állandó, folyamatosan változik. Ennek megvalósítására szolgál az amplitúdó burkológörbe generátor (envelope generator). Egy tipikus ADSR burkológörbe ábrája:

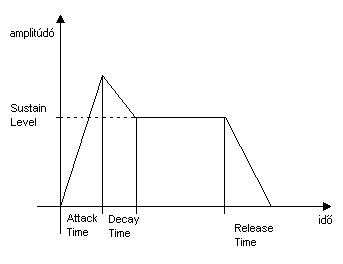
Az ábra egy tipikus ADSR burkológörbét ábrázol. Ez négy szakaszból áll. A felfutási (attack) szakasz ideje adja meg, hogy a hangszer a nulláról milyen gyorsan éri el teljes hangerejét. A lecsengési (decay) szakasz azt az időt adja meg, ami alatt a hangerő a maximumról a kitartási (sustain) szintre csökken, végül a felengedési (release) idő megmutatja, hogy a gerjesztés befejezése után a hangerő milyen gyorsan csökken a sustain szintről nullára. Természetesen bonyolultabb szintetizátorokban van lehetőség más burkológörbék kialakítására is (például a hang a gerjesztés időtartama alatt halk, majd a gerjesztés befejezésével hirtelen megnő a hangereje), de az ADSR az, amit minden szintetizátornak tudnia kell.

Mint már kiderült a valós hangszerek hangját vizsgálva, a hangerő és a felharmonikusok frekvenciája a sustain szakaszban sem állandó. Ennek, valamint a zenészek játékának megvalósítására szolgál a vibrato és a tremolo effektus. A tremolo effektus a hangerő kicsiny, periodikus változása, ez úgy valósítható meg, hogy az envelope generator vezérelhető egy alacsonyfrekvenciás oszcillátorral (LFO). A vibrato effektus pedig a hangmagaság kicsiny, periodikus változása, ekkor a lejátszási frekvenciát (azaz a transzponált frekvenciát) változtatja az LFO kimenete. Egyszerűbb szintetizátorok esetében az LFO jele egyszerű szinusz, azonban hatásosabb, ha az LFO háromszög, illetve fűrészfog jeleket is tud generálni.

A hangzás tovább javítható különböző effektusokkal, amik a zenét élőbbé, teltebbé teszik. Ilyenek a reverb (zengetés), a kórus, a flanger, az echo (visszhang) effektusok. Közös bennük, hogy mindannyian ún. késleltetés alapú (delay based) effektusok. Ha az eredeti és a késleltetett zenei jel között 150 ms-nál nagyobb a késleltetés, akkor az emberi fül már képes a két jelet szétválasztani, rövid visszhang hallható (un. Slap-back echo), mint egy üres szobában.

Ha a késleltetés kisebb 150 ms-nál, a fül nem képes a két jel szétválasztására, a két hang összeolvad, jellegzetes "kongó" hatás keletkezik, ez a zengetés. Igazán szép hatás akkor érhető el, ha a hangot többször (5-6-szor) késleltetjük, miközben az amplitúdó egy picit változik, így utánozható például egy templom akusztikája.

Megvalósítható az is, hogy egy bizonyos hely akusztikáját szimuláljuk. Ehhez szükség van egy vizsgálójelre, valamint arra, hogy ezt a jelet az adott helyen lejátszuk és rögzítsük. Az így nyert két jelből előállítható a helyre jellemző zengető-algoritmus. A kórus effektus annyiban különbözik a zengetéstől, hogy a késleltetett hangok hangmagasságát is változtatni kell kis mértékben, így olyan érzet keletkezik a fülben, mintha az adott hangszerből több szólna egyszerre. Flanger effektusnál pedig a hangmagasság (frekvencia) változtatása periodikusan történik egy LFO segítségével.

Ezek az effektusok viszonylag könnyen és gyorsan megvalósíthatók úgy, hogy a hangmintát memóriába írjuk, majd késleltetési idő múlva újra kiolvassuk, és lejátszuk (természetesen ekkor az effektusok használata a polifóniafok csökkenéséhez vezet, hiszen az effektus lefoglal egyet a rendelkezésre álló megszólaltatható hangokból), de a legtöbb szintetizátoron lehetőség van egy külső DSP csatlakoztatására.

Mindennemű algoritmusnál többet számít a szintetizáláshoz használt hangminták minősége, és mennyisége, csodát ugyanis ez esetben sem várhatunk: minél több mintát veszünk az eredeti hangszerről, a szintetizált hang annál jobb lesz. A DirectX a hetes verzió óta (a DirectMusic megjelenése) tartalmaz egy software wavetable szintetizátort, méghozzá nem is akármilyet: az algoritmusokért és a hangmintákért a Roland cég a felelős, őket talán nem kell bemutatni. Ezen kívűl a DirectMusic támogatja a DLS (Downloadable Sounds) szabványt, így nem kötelező a beépített hangmintákra támaszkodni, a végleges játék nyugodtan használhatja azokat a hangmintákat, amit zeneszerző a mű írásakor használt.

Az egyetlen gond (és ez a hangkártyagyártók számlájára írható), hogy jelenleg tudtommal (bármit is mondjanak) egyetlen hangkártya drivere sem támogatja a DirectMusic hardveres gyorsítását (pedig az SBLive!, a Vortex2, a Canyon3D, a Crystal kártyák mind megfelelőek lennének erre). A minőségről meg csak annyit: feltehetően mindenkinek tetszett a Drakan vagy a Hitman zenéje: mindkettő DirectMusic-ot használ...

[oldal:Hangszintézis - Fizikai modellezés]

Sokáig úgy tűnt, hogy a módszer a számítási teljesítmény növekedésével (és az árak csökkenésével) egyre inkább előtérbe kerül, kiszorítja a wavetable szintézist, ez azonban máig nem történt meg (sajnos, mivel igen élethű hangzást kaphattunk volna).

Ez a módszer gyökeresen eltér az eddigi szintetizálási módszerektől. Kifejlesztése a Stanford Egyetemen történt (és történik még ma is). A kifejezés abból adódik, hogy az igazi hangszer fizikai viselkedését, a létrejövő rezgéseket szimuláljuk egy olyan modellel, amiben ugyanazok a fizikai folyamatok zajlanak, mint az eredeti hangszerben. Ebből látható, hogy míg eddig a hangot magát próbáltuk utánozni, a fizikai modellezéssel a hang létrejöttének módját próbáljuk utánozni. Mint minden bonyolult struktúra modellezésénél, a hangszerek modellezésénél is jól használható a blokkokra bontás. A blokkokra osztás többféleképpen is elképzelhető:

• fizikai felépítés szerint egy hegedű például felosztható húrokra, húrtartókra, stb.
• funkcionális szempontból egy hangszer gerjesztőre (például vonó) és rezonátorra (húr és test) osztható
• egy-egy blokk leírható fehér- illetve fekete doboz megközelítéssel.

A fekete doboz megközelítésben a blokkokat a ki- és bemenetek viszonya (frekvencia- és fáziskarakterisztika, átmeneti függvény) határozza meg. Fehér doboz megközelítésben a blokkokat működési mechanizmusuk írja le, így sokkal rugalmasabb modellt kapunk, ám a megvalósítás is nehezebb.

A gerjesztések és rezonátorok modellezésére itt nem térnék ki (az már tényleg meghaladná e cikk kereteit), csak egyet említenék meg: a Waveguide modellek fizikai szintézis modellek, és ezt a Creative az AWE64-ben használta -- igaz csak szoftveresen, és nem is minden MIDI hangszernek volt meg a modellje -- de a későbbi típusoknál nem fejlesztette tovább.

Ma az egyetlen elérhető megoldás PC-re a Yamaha software szintetizátora, amely egyszerre egy hangszert képes fizikai modellezéssel megszólaltatni.

[oldal:Technikai jellemzők mérése - elmélet]

Itt most összefoglalnám, hogy milyen mérések szerepelnek a hangkártyatesztekben (és azok mit jelentenek), valamint -- amolyan példaként -- egy Gravis UltraSound PnP kártya eredményeit is megnézhetitek (csak tartsátok szem előtt, hogy az a kártya 1995-ben készült, ha jól emlékszem).

A mérésekhez használt kiegészítő kártya egy Terratec EWX24/96 (köszönet érte a Pixel Multimédiának), amelyen igen jó minőségű, 24 bites, 96kHz-es A/D és D/A átalakító található. Na ugorjunk neki!

Jel/zaj viszony, torzítás (SNR, THD, THD+N)

Mint már említettem a jel/zaj viszony (SNR) a jel és a zaj teljesítményének hányadosa decibelben (dB) kifejezve. Minél magasabb ez az érték, annál zajtalanabb egy rendszer.

A harmonikus torzítás (THD) a legnagyobb amplitúdójú frekvenciakomponens és az ezen frekvencia harmonikusain levő komponensek teljesítményének aránya, százalékban. Méréséhez 1 kHz-es szinuszos vizsgálójelet szokás alkalmazni, ekkor a harmonikusokon megjelenő komponenseket a rendszer torzítása szolgáltatja, minél kisebb, annál jobb. a THD+N (torzítás + zaj) ettől annyiban különbözik, hogy a harmonikusok teljesítményéhez a zaj teljesítménye is hozzáadódik a számításkor.

A/D vizsgálatoknál az EWX kártya a jelforrás (a kimeneti jelét digitalizálja a vizsgált kártya), a vizsgálójel pedig egy 24 bites, 1 kHz-es szinuszjel (a mért értékek a jobb felső sarokban, sorrendben: SNR, THD+N, THD):

Ezen az ábrán (és ha nem jelzem külön, akkor a továbbiakban is) az átfogott amplitúdó tartomány 200 dB, a frekvenciatartomány pedig 0-20 kHz.

D/A vizsgálatoknál a forrás maga a vizsgálandó kártya, az EWX ennek a kimeneti jelét digitalizálja. A vizsgálójel (legalábbis amig 16 bites kártyáról van szó) egy 16 bites szinuszjel (még mindig egy 1 kHz-es):

Intermodulációs torzítás (IMD)

Intermodulációs torzítás akkor lép fel, ha egy rendszerbe több komponensű (jelen esetben kettő) jel kerül. Ekkor megjelennek olyan nemkívánatos komponensek, amelyek a két komponens modulációjából, összekeveredéséből származnak. Az IMD ennek a torzításnak a mértékét mutatja meg, minél kisebb, annál jobb.

A/D vizsgálatnál a vizsgálójel 24 bites, a két frekvenciakomponens 250 és 8020 Hz-en található, utóbbi amplitúdója 4 dB-vel kisebb (a mért eredmény szintúgy a jobb felső sarokban).

D/A vizsgálatnál a jel 16 bites:

Átvitel

Itt tulajdonképpen a hangkártya amplitúdóátviteli függvényét mérjük (igaz csak egyes frekvenciákon). A vizsgálójel sok különböző frekvenciájú szinuszjel összege.

Itt az átfogott amplitúdótartomány 0,2 dB, és még ilyen felbontás mellett sem látható eltérés az egyes frekvenciakomponensek amplitúdója között (ezért jó vizsgálójel ez).

[oldal:Technikai jellemzők mérése - gyakorlat]

Most pedig nézzük egy tesztben hogyan köszönnek vissza ezek az erdmények (az itt vizsgált kártya -- mint már említettem -- egy Gravis UltraSound PnP -- lerójuk tiszteletünket eme brilliáns cég előtt :)). Ezek az értékek összehasonlítási alapnak is jók, látahó lesz mennyit fejlődtek a kártyák 6-7 év alatt (túl sok kommentárt nem fűzök az ábrákhoz).

Jel/zaj viszony, torzítás -- A/D

Az átfogott amplitúdótartomány 140 dB, de azt hiszem ez még látszik is.

Intermodulációs torzítás -- A/D

Csak hogy egy kicsit kavarjak -- itt most 150 dB a teljes amplitúdóskála.

Átvitel -- A/D

Az amplitúdótengely itt 2 dB tartományt ábrázol, látható hogy a kártya átvitele ezen belül marad.

Jel/zaj viszony, torzítás -- D/A

Az átfogott taromány 170 dB (ezt majd egységesítem :)). Azt még megjegyezném, hogy a szintetizátor rész kikapcsolásával a jel/zaj viszony jelentősen javítható -- úgy tűnik ennek D/A-ja picit zajosra sikeredett (ami mellesleg fülhallgatón is remekül hallható).

Intermodulációs torzítás -- D/A

Még mindig 170 dB.

Átvitel -- D/A

Itt 4 dB az átfogott tartomány, ennyit ingadozik a kártya átvitele, és ez sajnos már nem túl jó érték.

Csak azért hogy lássatok valami igazán jó minőségűt is, következzen a mérésekhez használt EWX kártya átvitele loopback módban (azaz a kártya kimenete a saját bemenetére van kötve):

Az ábrázolt tartomány 0,3 dB, és mint látható az átvitel 0,1 dB-t ingadozik !!! Ez minőség (egyébként hallhatóan szebb hangja van, mint bármely más kártyának ami valaha megfordult nálam, és mellesleg itt sikerült megoldani, hogy a számítógép zajait egyáltalán nem szedi össze, és saját alapzaja sincs).

[oldal:Rövidítések, szabványok, cégek áttekintése]

Már csak egy dolog maradt hátra: a felmerülő rövidítések, szabványok, cégek rövid ismertetése.

A3D: Az Aureal saját 3D hang API-ja (application programming interface) még akkor keletkezett, amikor DirectSound3D nem nagyon volt. Mindenféle kiegészítés nélkül "csak" 3D hangok térbeli pozicionálását képes kezelni. Az A3D-DS3D wrappereken keresztül a legtöbb A3D játék DS3D kártyákon is hajlandó működni.

A3D 2.0, 3.0: Az előző API továbbfejlesztett változatai, amelyekben az Aureal saját megoldását építette be a környezet modellzésére, ez pedig a WaveTracing eljárás. Lényege, hogy minden hangforrásból 6 hang útját követi, számolja a környezetben levő tárgyakról a visszaverődést, és így végül azt, hogy a direkt úton kívül milyen visszavert hangok jutnak a hallgatóhoz.

Hátránya, hogy erőteljes programozást, sok erőforrást kíván (és az a 6 visszavert hang sem túl sok). A 3.0-ás változat még mp3-ak kezelésére is képes. Köszönhetően az Aureal által készített A2D drivereknek, a DS3D (és EAX) kompatibilis kártyák a legtöbb feladatot képesek hardveresen gyorsítani.

DirectSound: A DirectX hangvisszajátszásért felelős része. A DirectX előtti Windows-os megoldáshoz képest legnagyobb előnye az igen kicsi késleltetés és a hardveres gyorsítás támogatása.

DirectSound3D: A DirectX 3D hangzással kapcsolatos része. 3D hangkártya esetén hardveres gyorsítás használható, ennek hiányában többféle szoftveres megoldást támogat (amit persze senki sem használ).

EAX 1.0: (Environmental Audio Extension): A Creative Labs által kiagyalt, majd a DirectX-be kiterjesztésként beépített szabvány, a környezet szimulálására szolgál. Az A3D-vel ellentétben nem az egyes hanghullámok útját követi, hanem a környezetet statisztikusan modellezi (elsősorban az "early reflections" (gyorsan bekövetkező visszaverődések) és a "late reverb" (későbbi visszaverődések) segítségével, de igen sok paraméter állítható).

EAX 2.0: Megjelent az előző verzió nagy hiányossága: az "occlusions" és "obstructions" kezelése. Eme két funkció tulajdonképpen elég hasonló: az első esetben azt modellezik, hogy a hangforrás más térben van, mint a hallgató, míg a második esetben a hangforrás és a hallgató közti közvetlen úton van valami akadály, ezért nem hallhatók a direkt hangok, csak a visszavertek. Sajnos mostanáig nem sok játék használja ki az EAX2-t (ehhez azért több tervezés kell).

Sensaura: A Sensaura egy angol illetőségű cég, amely 3D algoritmusok kidolgozásával és licencelésével foglalkozik, tehát nem szabvány, csak gyártó. Partnerei között megtalálható a Crystal, az ESS, és a Yamaha.

MacroFX: A Sensaura egyik technológiája, mely az igen közeli (egy méteren belüli) hangforrások pozicionálását javítja. Használata nem igényel támogatást a programok részéről.

ZoomFX: A Sensaura másik ötlete, a hangforrás kiterjedését próbálja szimulálni. Sajnos programozói támogatást igényel, így meglepne, ha elterjedne (jelenleg senki sem használja).

VirtualEAR: Még mindig a Sensauránál maradva, újabban lehetőség van arra, hogy a Sensaura 3D algoritmusokat a fejünkhöz hangoljuk, ennek a programnak a segítségével.

QSound: A QSound Labs, csakúgy mint a Sensaura, 3D-s algoritmusokat gyárt (többek között) és azokat licenceli. Vásárlóik között a Philips-t és a Fortemediát találjuk.

A Sensaurán és a QSoundon kívül még saját algoritmusa van az Aurealnak és a Creative-nak (bár most már az Aureal is a Creative tulajdona).

Remélem, sikerült egy messze nem teljes, de a lényeget talán tartalmazó összefoglalást adni a PC-s hangkeltés világáról (és azt is remélem, nem volt teljesen érthetetlen :)). Természetesen előfordulhat a cikkben hiba, illetve az is hogy valami nem érthető. Ezt nyugodtan jelezzétek az e-mail címemre, vagy mondjátok el észrevételeiteket a fórumban.

És még mielőtt bárki plágiummal vádolná a HWSW-t, a cikk a SavageGamers-en megjelent (általam elkövetett) írás engedélyezett közlése.

Szólj hozzá a fórumban!